基于BP神经网络的氢气传感器数据拟合与研究

        0 引 言

        随着国家对新能源的大力提倡，氢能源逐渐走进大众视野。氢气作为一种高效清洁的二次能源，与其他能源相比（如天然气），氢气燃烧后并不会产生温室气体，具有更好的应用前景。现阶段随着氢燃料电池技术的突破，氢能源已经开始应用到混合动力汽车、火箭推进剂和各种化工领域[1]。同时，我国也开始加大对氢燃料电池领域的支持力度，《中国制造2025》提出到2025年，制氢、加氢等配套基础设施基本完善，燃料电池汽车实现区域小规模运行。但是由于氢能源的易燃易爆性，它的安全性问题必须得到重视，其制备、储存、运输和应用中都要防止泄露引起的爆炸，这就需要大量的氢气传感器投入检测，而提高氢气传感器的灵敏性、选择性和稳定性一直是传感器领域重要的研究方向。

        目前国内外学者对气体传感器的算法优化已经开展了相关研究，黄兵等将分段幂函数模型应用于气敏检测器定量算法中，一定程度上提高了检测的精度[2]。周长林等提出一种基于局部多项式回归的气敏传感器模型优化算法，消除了非目标参量的影响，但多项式回归的逼近程度还有待提高[3]。文献[4]将BP神经网络应用于甲醛测量仪的设计，但并未对预测误差进行分析。蔡晶晶等提出基于BP神经网络的温度传感器辐射误差分析，为误差校正和本文的研究提供了参考[5]。综上，目前气体传感器的检测中灵敏度仍然偏低，而神经网络算法在改善和提高传感器性能方面具有巨大潜力。

        本文以简化传统传感器的调理电路为目标，首先分析了传感器检测电路的工作原理，计算了传感器电参数的表达式；然后介绍了最小二乘曲线拟合法和BP神经网络的基本原理；最后比较了灵敏度系数与氢气浓度的拟合方程与BP网络模型的预测精度。仿真结果表明，利用BP神经网络建立的测量模型能够实现对气体浓度更为精确的预测。

        1 传感器的等效检测电路

        1.1 基本检测电路

        气敏传感器的本质在于其电导率会随着环境中所测气体的浓度发生改变。对于采用半导体材料制备的氢气传感器而言，当处于清洁空气中时，半导体材料的电导率较低；当处于一定浓度氢气的环境中，附着在半导体材料表面的氢气分子会发生相应的化学反应，使得气敏材料的电导率增大，并且电导率会随着氢气的浓度增加而继续增大[6]。因此，通过设计合理的测量电路可将传感器电导率的变化转换成对应氢气浓度下的输出信号。

        实验中并不能实时测量传感器自身阻值的变化。为提高测量精度，在传感器外部串联一个负载电阻，将传感器电导率的变化转换成负载电阻上电压的变化，作为传感器对外输出的模拟信号。图1为氢气传感器的基本检测电路，图中各参数的含义如表1所示，加热电阻RH的作用是为传感器的正常工作提供一定的温度。

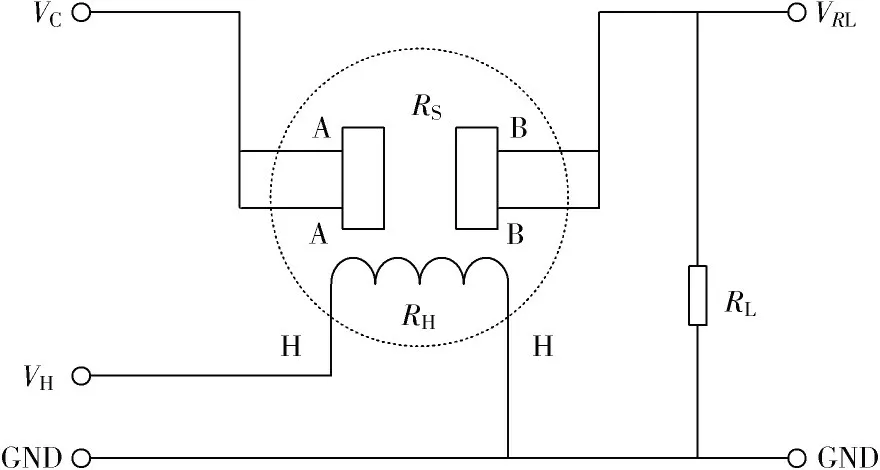
        图1 氢气传感器基本检测电路

        表1 氢气传感器检测电路的电参数

        1.2 检测电路的计算

        基于检测电路的分析，可以得到传感器等效电阻RS与输出电压VRL间的表达式。图1中流过负载电阻的电流为VRLRL，串联负载RL后，总电阻为VCIRL，因此传感器等效电阻RS可以表示为：

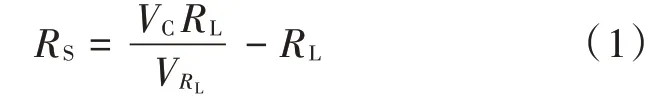
        气敏材料的功耗PS可通过式（2）表示，即：

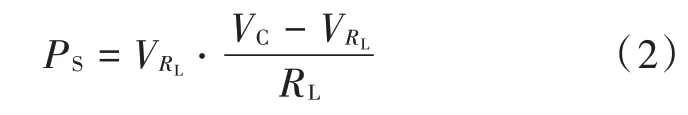
        由式（1）可知，通过测量负载电压即可确定传感器的阻值RS，同时负载电阻的取值也会影响到RS和PS，因此为获得更好的实验效果，测量时应选择合适的负载电阻RL。

        灵敏度系数作为衡量传感器工作性能的重要指标，其表达式为：

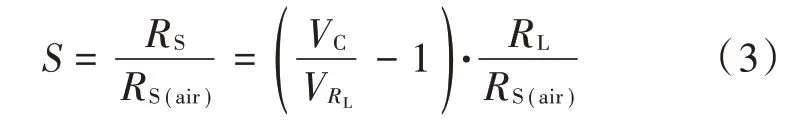
        式中，RS（air）为氢气传感器在清洁空气中的基准阻值，取值范围[7]为5～20 kΩ。为计算方便，本文选择RS（air）=5 kΩ。

        2 曲线拟合与BP神经网络的原理

        2.1 曲线拟合

        所谓的拟合就是用一条平滑的曲线将平面分散的点连接起来，选择与这些散点分布较为接近的曲线方程来表达两个或多个变量之间的变化规律。最常用的拟合方法为最小二乘曲线拟合法[8]：通过将误差的平方和降至最小从而匹配到与散点分布最相近的函数方程。

        设定已知的k个离散点的坐标为{(xi,yi),i=1,2,…,k}，假设这些点逼近的函数为y=f（x）。当f（x）为线性函数时，称为线性拟合；当f（x）为非线性函数时，称为非线性拟合，常用的非线性拟合有指数拟合、对数拟合和幂函数拟合等。定义残差ei为：

        将残差ei的平方和进行最小化处理，即：

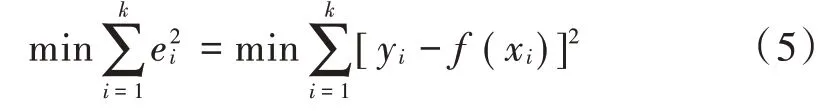
        对于线性拟合，设逼近函数f（x）=ax+b，即寻求a和b使残差的平方和最小，由最小二乘法[9]可确定系数a和b为：

        非线性拟合可通过变形等方法转化为线性拟合，例如对于标准幂函数f（x）=cxd，可同时在等式两边取常用对数，如下：

        即当散点满足以lgyi和lgxi坐标系呈直线趋势分布时，可采用幂函数拟合分析两者之间的关系。

        2.2 BP神经网络

        图2 为本文采用的BP神经网络结构，包含输入层、隐含层和输出层。设输入层神经元的个数为I，隐含层神经元数目为J，输出层神经元数量为K，隐含层使用S型传递函数tansig，输出层采用线性传递函数purelin。BP神经网络主要包括信息向前馈入与误差反向传播两部分[10]。

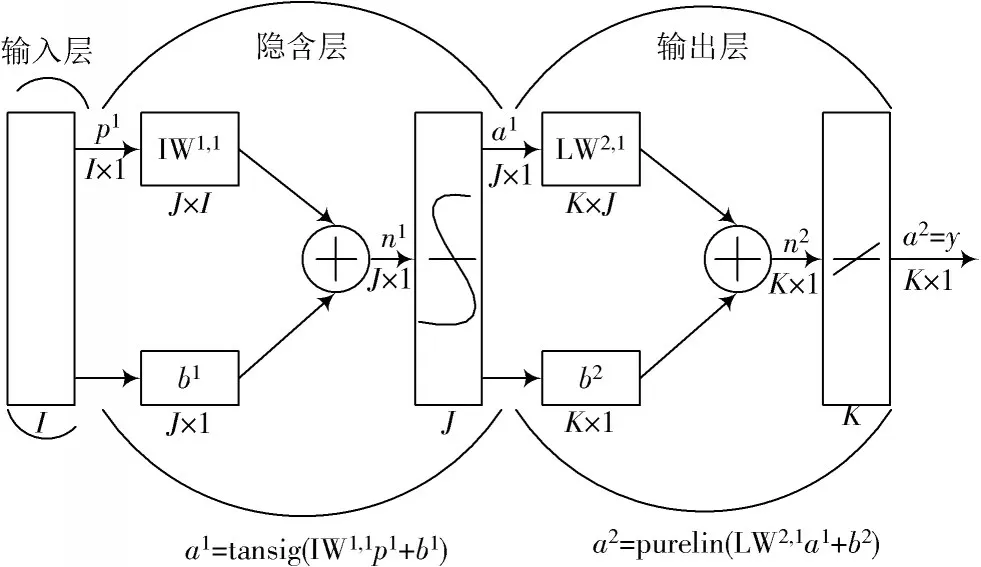
        图2 三层BP神经网络结构

        1）信息向前馈入

        样本依次经过输入层、隐含层和输出层被处理，即输入样本I=[I1，…，Ii，…，II]经过隐含层后转换成H=[H1，…，Hj，…，HJ]，再经输出层计算为O=[O1，…，Ok，…，OK]。其中隐含层神经元输出Hj为：

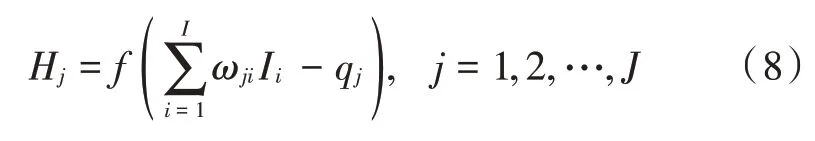
        式中：ωji为隐含层节点j与输入层节点i连接权值；qj为隐含层节点j的阈值；f（·）为隐含层传递函数。

        输出层神经元的输出Ok为：

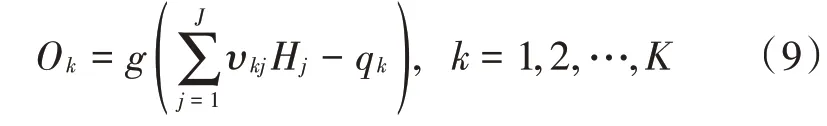
        2）误差反向传播

        当输出层的输出值与期望值之间的误差不满足精度要求时，误差由输出层反向传播至隐含层和输入层，逐层调整权值和阈值，使得输出的预测值与期望值之间的误差逐步减小，最终下降到要求精度范围内[11]。设为输出层节点k的期望值，则输出值与期望值的误差E为：

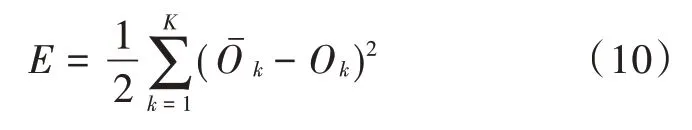
        结合式（9）和式（10），可得误差函数E为：

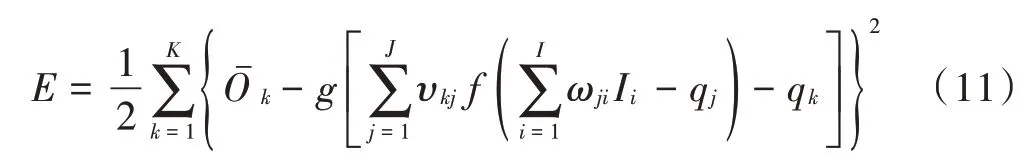
        分别求误差E对输入层与隐含层神经元间的权值ωji和隐含层与输出层神经元间的权值υkj的偏导数，即：

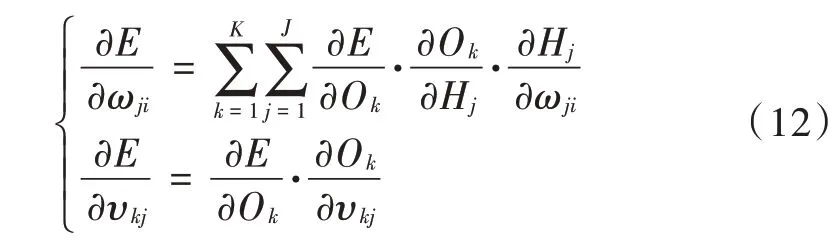
        得到每次迭代中权值的调整公式为：

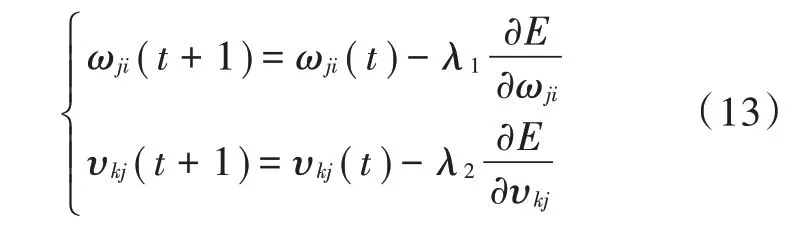
        式中：t为迭代次数；λ1和λ2分别为隐含层和输出层的学习效率。

        同理，也分别求取误差E对隐含层神经元阈值qj和输出层神经元阈值qk的偏导数，从而得到阈值的调整公式qj（t+1）和qk（t+1）。每次迭代中权值和阈值的调整都是沿着负梯度方向进行的，即可使误差函数E下降得最快。

        2.3 评价指标

        为评价曲线方程的拟合能力和BP神经网络的性能，首先引入相对误差error，它反映了预测值偏离真实值的实际大小，其计算公式如下：

        后事件同步机制是一种被动时间同步协议[13]。假设节点在T13时刻后检测到枪声事件，记录事件触发的时间T14。在同步周期较短的情况下，估算节点和簇头的相对频率偏差ais[14-15]。此刻对应簇头的本地时钟为ais(T14-T13)+T13，簇头收到节点数据之后根据各节点检测信息完成算法融合。

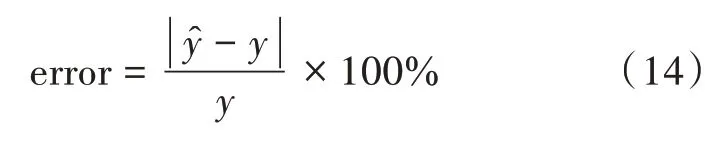
        其次引入整体性评价指标R2，在拟合中R2称为拟合优度，用于衡量回归方程的拟合度；在BP算法中称为决定系数，用于评价网络模型的泛化能力。根据文献[12-13]，R2的定义式如下：

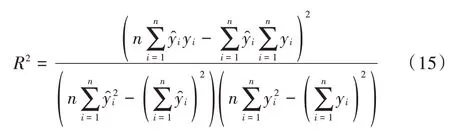
        3 传感器测量模型的建立

        3.1 测量数据分析

        要建立传感器的测量模型，首先要获得传感器的输出响应与对应气体浓度的测量数据。本文使用MQ-135气体传感器搭建实验平台，实验中采用5 V直流电源供电，传感器串联的负载电阻RL选取为10 kΩ，负载电压输入到数字示波器，实时显示电压的变化。氢气浓度的测量采用高精度氢气检测仪，量程为0～1 000 ppm，分辨率为0.1 ppm，测量误差小于±3%FS。图3获取了40组不同氢气浓度下负载电阻的电压值。

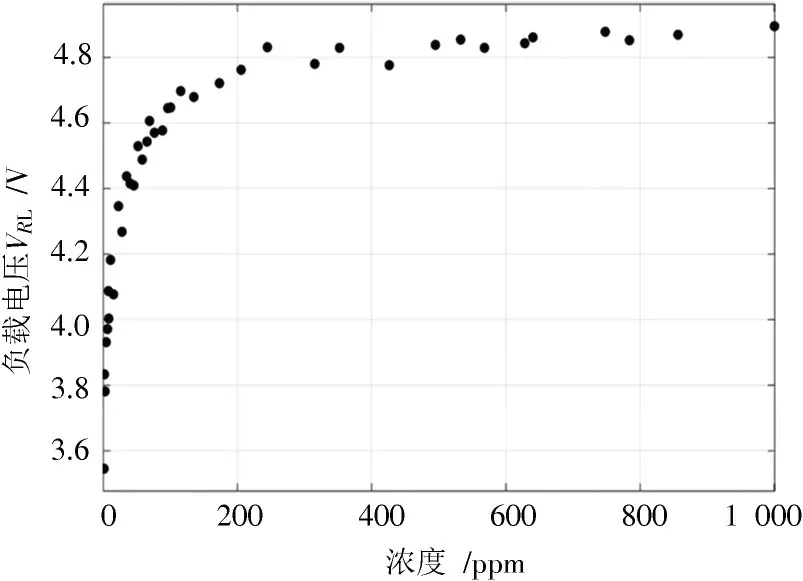
        图3 不同氢气浓度下传感器负载电压的散点分布

        3.2 数据拟合

        结合负载电压测量结果和式（3），对40组不同氢气浓度下对应的灵敏度系数进行计算，通过对数据进行拟合意得到两者的变化规律，从而建立传感器输出响应与浓度的模型。图4为使用Matlab拟合得到的灵敏度系数S与氢气浓度CH2的幂函数拟合曲线。

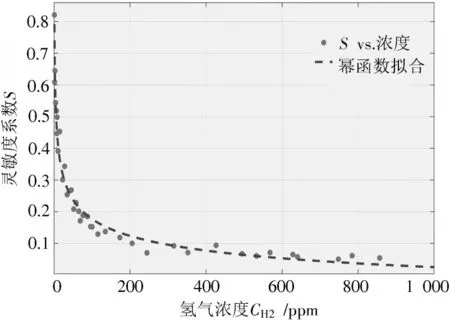
        图4 氢气浓度与灵敏度系数的拟合函数曲线

        拟合中采用幂函数与常数项相加的方式，表达式如下：

        式中：a1=1.032；b1=-0.196 8；c1=-0.240 2。拟合的误差平方和SSE为0.037 82。

        通过幂函数拟合式（16）可推导出CH2随S变化的函数表达式：

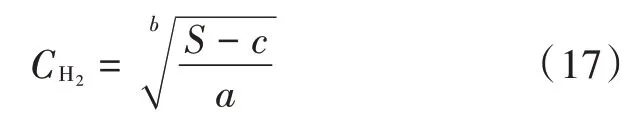
        在氢气浓度有效范围内，随机取5组数据，将拟合测试结果与实际测量值进行对比，如图5所示。可知数据拟合值与实测值2条折线走势基本一致，但个别样本差距较大，整体的拟合优度R2=0.978 72，较为接近于1。

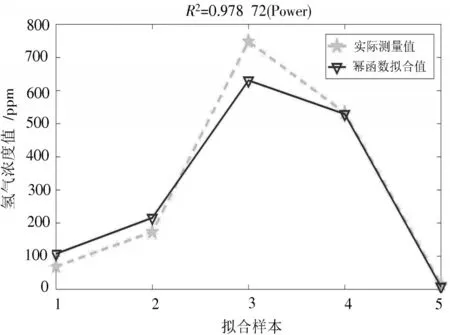
        图5 幂函数拟合结果与实际测量值的对比

        3.3 BP算法训练

        通过建立BP神经网络模型对采集的40组数据进行训练预测。训练中将灵敏度系数S作为输入变量，氢气浓度CH2作为输出变量，随机产生35组数据作为训练样本，剩余5组数据作为测试样本，隐含层神经元个数选取为10。设置训练次数为1 000次，期望输出与实际输出的偏差最小为1×10-3，当两者输出的偏差E≤Emin或训练次数达到1 000次时，结束此训练过程，学习速率λ均取为0.01。

        图6 所示为BP神经网络模型输出的氢气浓度预测值与实际测试值的对比。可知在所预测的5个样本中，BP预测值和测量值的折线十分接近，且决定系数R2为0.999 62，非常接近1，表明BP神经网络对氢气浓度的预测更为精确。

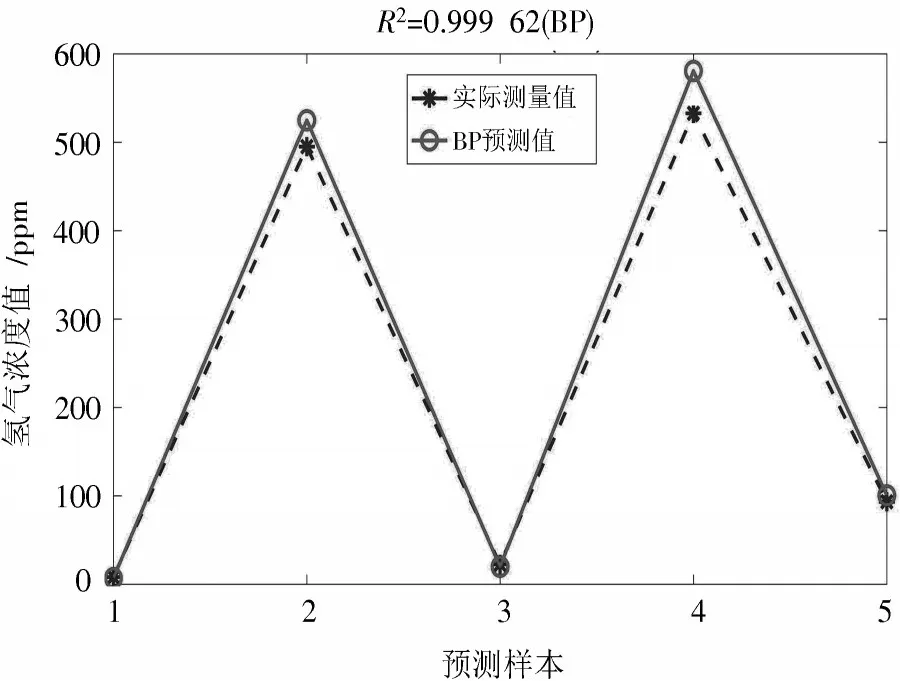
        图6 幂函数拟合结果与实际测量值的对比

        3.4 测试误差对比

        图7 给出了5组拟合样本与BP网络预测样本的相对误差对比。分析图7可知：拟合样本的相对误差波动幅度较大，样本整体的平均误差为29.28%；而BP神经网络的预测样本中，每组的相对误差均降至较低的水平，且平均相对误差为9.74%，较拟合样本的相对误差降低了19.54%，预测精度明显提升，说明通过对数据进行简单的公式拟合并不能正确反映两者之间的关系，而BP网络模型对氢气浓度的预测具备更优的泛化能力。

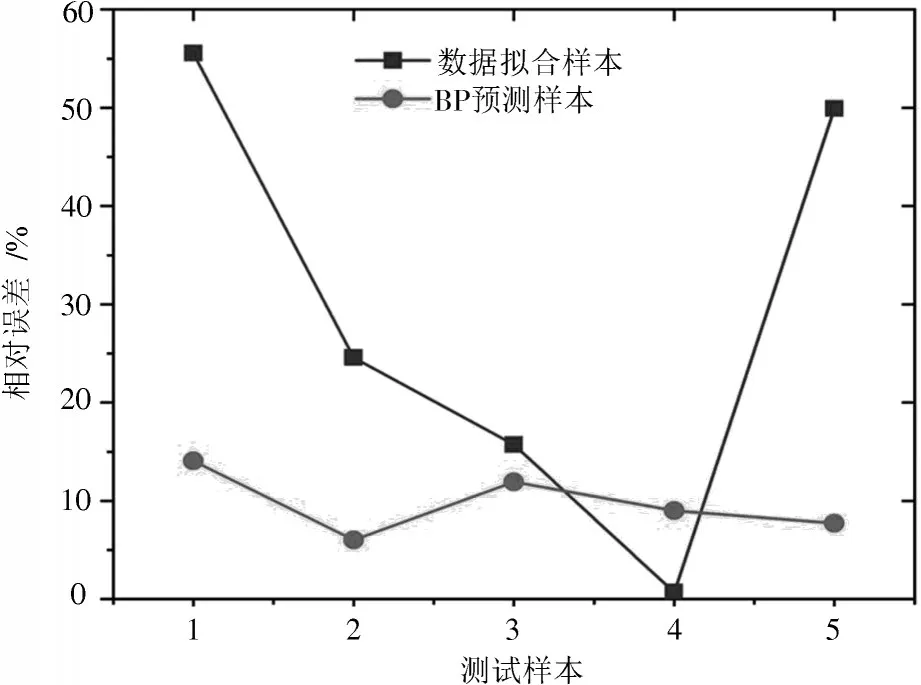
        图7 数据拟合与BP预测的误差对比

        4 结 语

        本文提出将氢气传感器的测量电路与BP神经网络训练算法两者结合的思路，意图构建更加准确的传感器的测量模型。首先，通过对测量数据进行幂函数拟合，得到气体浓度与传感器灵敏度系数的逼近方程，测试样本的相对误差达到29.28%，拟合优度为0.978 72。为进一步提升预测精度，将测量的传感器输出响应和对应氢气浓度数据送入BP网络训练，输出氢气浓度的预测值与实际值，对比可知网络模型的R2高达0.999 62，平均误差降至9.74%，与拟合测试样本相比，BP预测值的相对误差减小了19.54%，R2提高了2.14%。结果表明BP神经网络模型具有更好的泛化能力。通过检测传感器的输出响应即可实现对氢气浓度的高精度预测，极大地简化了传统传感器的信号调理电路。